Ildikó Ferencziné Ács, Hungary
As a result of technological progress, MIDI recordings and digital choral parts are available to choir leaders to facilitate the rehearsal and learning process. However, what on the one hand seems modern and innovative (digital pianos, audio and video recordings, streaming, virtual choirs) can have a negative impact on the other.
The following chapters will point out why reading music with a relative system of solfa is beneficial, and why learning to sing a part or a choral work with the help of piano is less supported.
The role of the piano in the learning process
The piano or the digital or virtual keyboard instruments are basically tempered.[1] This means a sort of equal temperament, where the 12 semitones of the octave are exactly at the same distance from each other. Alexander John Ellis, a 19th-century English mathematician and linguist, developed a new system and unit of measurement for comparing the different temperaments and the pitches they could produce. Using the cent system, he transformed the 2:1 ratio of the octave into a linear scale of 1200 degrees, where intervals can be described by arithmetical differences. The semitone as the smallest pitch interval was defined as = 100 cents (the cent is the hundredth of a tempered semitone), while whole tones correspond to 200 cents. In fully equal tuning, all keys are of equal value (Ferencziné, 2015).
Figure 1. The cent system
Related to the question of how to achieve pure singing and to the use of instruments it needs to be observed that “it is well known that any kind of temperament […] is alien to the pure intonation of the choir.” One can use a piano to play a starting and a control note, as a kind of reference point, i.e., only playing notes that are the same (perhaps in the same octave). “The part sung by the choir should never be struck on the piano. […] The instrument is only for the purpose of constantly relating the sound to its starting point” (Kardos, 1969: 29). The human singing voice is interpreted only in an acoustic context.
Properties of the acoustic overtone series
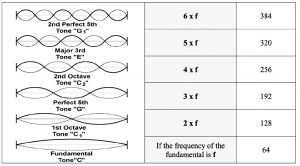
The human voice, the singing voice as a sound source, can be interpreted as an acoustic signal. When, for example, a string or a vocal cord vibrates, not only the fundamental is heard, but also its frequencies multiplied by whole numbers: its harmonic overtones. The frequency relationships are represented by the successive notes of the overtone series:
Figure 2. Overtones [2]
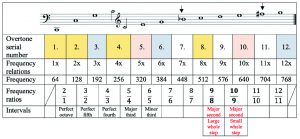
The following figure shows a series of overtones projected onto the great C/C2 (overtones 7 and 11 are deeper than the notes used in the diatonic framework), with the frequency values and ratios associated with the notes below. Colours are used to denote octaves built upon each other.
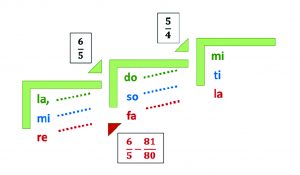
In the score of the overtone series, major seconds can be seen between overtones 8 and 10. Playing these on the piano means two whole tones of the same size. However, it is clear from the proportions below the intervals that the first interval, 9/8, is wider than the second one, which is 10/9. To distinguish between the two types of major second, we use the terms 9/8 “large whole step” and 10/9 “small whole step.” The frequency ratio of the two whole notes is 81/80, corresponding to ≈ 22 cents.
Comparing the three types of whole tones (major second), the differences in size become apparent.
Figure 4. a-b. The three kinds of major seconds
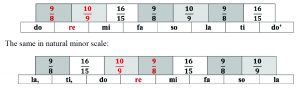
The difference between large and small whole steps arising from the difference in acoustic frames is also clearly visible. In the major key, the seconds follow each other in the following order:
The same in natural minor scale:
Figure 5. a. Major key; b. Natural minor key
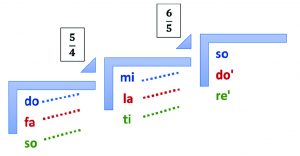
On the basis of Figure 3, examining the thirds in the overtone series and the role and behaviour of the notes in the diatonic scale, we can depict the structure of the major triads as follows:
Figure 6. Major triads of the diatonic scale
All the chords have a pure major third and minor third structure. It is no coincidence that these have become the most stable and strongest triads of the major key, the major triads, the carriers of the main functions.
All but one of the minor chords of the diatonic system also sound clear. Only in the minor triad with a re root is the semitone forming the minor third paired with the 10/9 small whole step, i.e., the minor third is narrower in this case by a ratio of 81/80.
Figure 7. The minor triads of the diatonic scale
It is therefore clear that the re note is in a sensitive place, depending on its position and tonal location. The position of a note in a given tonality, its role, the stability of the pure intonation of different intervals and harmonies, can be developed through practice. A learning process is effective if “constant” elements occur frequently among the ones to be learned. The more variables there are, the more unstable the memorisation of the turn to be learnt becomes, and the longer the process of deepening takes. Of the two types of solfa systems, absolute and relative ones (also known as “fixed do” and “movable do”), only one is capable of satisfying the above learning process, and that is the relative system.
The role of relative solfa in the development of clear intonation
The learning of tonal music pieces and the clear intonation of melodies and harmonies are ensured by relative solfa. The name of a melody’s notes, the distance between two notes with the same name, and their role in the tonality are constant. For example, in a major key, a so-re-mi turn always has a descending perfect fourth and an ascending major second, whatever the key we are in. With absolute solmization, however, the width of the intervals can vary, even with the same name.
Figure 8. Relative solfa – absolute solfa
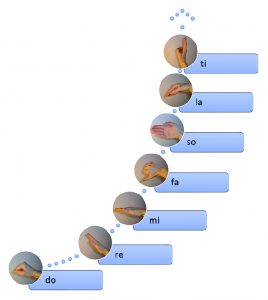
In a tonal musical context, the most suitable method for achieving and practising pure intonation is therefore the use of relative solfa. Automatic use requires a lot of practice, and one of the tools of this is the use of hand signs. Due to their spatial positioning, they offer an excellent opportunity to specify pitches in the right direction and to show the sensitivity of the notes.
Figure 9. Hand-signs
Monophonic examples
Pure singing can only be achieved through the interaction of monophony and simultaneous voicing, the foundations of which must be laid in monophony. When pointing out the difference in width between the large whole step and small whole step, let us make others aware that in both major keys and natural minor keys, whole steps occur between the following degrees of the scale:
1-2.
4-5.
6-7.
From an intonation point of view, therefore, particular attention should be paid to intoning and sustaining the 2nd, 5th and 7th degrees high (Kardos, 2007):
do-fa-so; so,-do-re; mi-la-ti; la,-re-mi
where the ascending second in a fifth ambitus should be intoned high, or the small whole step turns:
do’-la-so; la-so-mi; re-do-la,; so-mi-re
in which the descending seconds should be intoned high in a fourth ambitus.
Particular attention should be paid to the intonation of the two kinds of re. This can be practiced in a tune example as shown in the following chart:
Although we have used the term “low re” in the minor key, in practice we feel that the do and the mi are higher, more tense, and the re is deeper in comparison.
The two kinds of seconds can be illustrated by different colours in the following sheet music example:
Figure 10. Alleluia[3]
Polyphonic examples
In his booklet Let us Sing Correctly (1941), Zoltán Kodály proceeds in the order of the acoustic overtone sequence, voicing the octave and fifth intervals, and then in fourths to the sounding of the thirds.
Figure 11. Overtones
However, this sound order cannot be generalised to all choir types and age groups. The perfect fifth and the perfect octave can indeed be defined as the starting point for teaching pure intonation in male choirs, but for female and children’s choirs, due to the relative scarcity of overtones resulting from the higher pitch of the fundamental, it is not advisable to start from these intervals. In the case of female and children’s choirs, the two kinds of thirds are the most suitable intervals for the beginning, especially the so-mi and then the mi-do relation (Kardos, 1969). It is therefore no coincidence that the introduction of the tonic major and, almost in parallel, the minor triad is practised first, especially for mixed choirs. After practising the intervals that make up the triad, it is recommended to intone the perfect fourth below the root (lower so). This is followed by conscious practice of the seconds.
Examples:
Figure 12. Major triads
The example above shows one possible way of combining the three major triads illustrated above in three parts. After the root note is voiced as a solid, firm base, the soft fifth should be played, followed by an even more mellow third. The voice leading is then carried on in second steps, where attention must be paid to the high intonation of the notes la and re.
So-related high re:
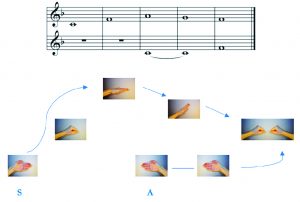
An example shown using hand signs (according to position in the chorus: soprano on the left, alto on the right):
Figure 13. Hand-signs in major tonality
Schubert’s Mailied clearly shows the behaviour of the re in major: above the lower so, the re is to be intoned high:
Figure 14. Schubert: Mailied [4]
La-related deep re:
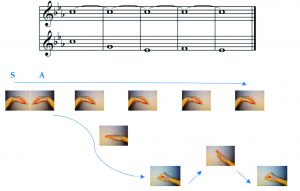
An excellent way to practice is when the other part is matched to a sustained note. This offers a chance to relate intervals to a constantly fixed point. The exercise below demonstrates this in minor tonality, using hand signs:
Figure 15. Hand-signs in minor tonality
In the case of a low re with a relation to la, the most important thing to pay attention to is the pitch of the following tone. E.g., la,-mi-re-do or la,-do-re-mi. That is, in the first example it is important to achieve a narrower second, in the second one, to achieve a wider second.
Figure 16. Lassus: Ipsa te cogat – excerpt
The role of the re in the tonality and the proximity of the notes la or so and the effect of these latter sounds often render it difficult to make a theoretical decision. The frequent changes are influenced by the musical context, the leading of the part and harmonic thinking together.
Summary
For clear singing, it is best if the melodic elements can always be voiced with the same names and syllables, regardless of the key, according to their role in the tonality. The same distance, step or jump can only be given the same name in the relative solfa system. Within the framework of a given tonality, the intonation of the intervals becomes stable and well controllable (Ferencziné, 2015).
 Ildikó FERENCZINÉ ÁCS, DLA, dr. habil. (b. 1966) is professor and head of the Institute of Music at the University of Nyíregyháza. She obtained degrees as Classroom Music Teacher, Teacher of Music Theory, Choir Conductor, and Teacher of Classical Singing. She studied Choir Conducting and received her DLA degree and received her training at the Franz Liszt Academy of Music in Budapest. She graduated as a singer from the Debrecen Conservatory of Franz Liszt Academy of Music. She has been teaching at the University of Nyíregyháza since 1989. She was the conductor of Gaudemus Choir of the University from 1993 until 2010. She worked as vice-dean of the Faculty of Humanities and Arts from September 2007, and as dean between May 2008 and September 2013. She carried out the functions of the vice-rector for education at the University of Nyíregyháza between January 2017 and June 2019.
Ildikó FERENCZINÉ ÁCS, DLA, dr. habil. (b. 1966) is professor and head of the Institute of Music at the University of Nyíregyháza. She obtained degrees as Classroom Music Teacher, Teacher of Music Theory, Choir Conductor, and Teacher of Classical Singing. She studied Choir Conducting and received her DLA degree and received her training at the Franz Liszt Academy of Music in Budapest. She graduated as a singer from the Debrecen Conservatory of Franz Liszt Academy of Music. She has been teaching at the University of Nyíregyháza since 1989. She was the conductor of Gaudemus Choir of the University from 1993 until 2010. She worked as vice-dean of the Faculty of Humanities and Arts from September 2007, and as dean between May 2008 and September 2013. She carried out the functions of the vice-rector for education at the University of Nyíregyháza between January 2017 and June 2019.
Works Cited
- Kardos Pál (1969): Kórusnevelés, kórushangzás. Zeneműkiadó. Budapest.
- Kardos Pál (2007): Egyszólamúság az énekkari nevelésben. Kardos Pál Alapítvány, Szeged.
- Kodály Zoltán (1941): Énekeljünk tisztán. Magyar Kórus Művek. Budapest.
- Ferencziné Ács Ildikó (2015): Intonáció – szolmizáció. In.: Ferencziné Ács Ildikó – Pintér-Keresztes Ildikó: Pótvonalak. SZAKTÁRNET. Nyíregyházi Főiskola. pp. 37-47.
- Fiala Péter (2015): A hangszerek fizikája. Jegyzet. BME, Budapest.
Edited by Taylor Ffitch, USA
[1] Andreas Werkmeister, a 17th-century organist, composer and theorist, who developed the technique of temperament, divided the pure octave into 12 equally spaced parts.
[2] Source: https://www.soundsnap.com/blog/glossary/overtone/
[3] Source: https://gregobase.selapa.net/chant.php?id=1341
[4] Source: https://imslp.org/wiki/Mailied,_D.199_(Schubert,_Franz)